Algoritmi in Python: Esempi e Applicazioni nel Mondo Reale

Hai presente quella sensazione di magia quando il tuo navigatore trova la strada più veloce in mezzo al traffico o quando Spotify ti suggerisce una canzone che sembra leggerti nel pensiero? Ecco, dietro a quella “magia” ci sono loro: gli algoritmi. E sai una cosa? Python, quel linguaggio di programmazione così versatile e amichevole, è uno strumento fantastico per dar vita a questi “geni della lampada” digitali.

Ma cosa sono esattamente gli algoritmi? Immaginali come delle ricette super dettagliate che un computer segue per risolvere un problema o raggiungere un obiettivo. Possono essere semplici, come trovare il numero più grande in una lista, o incredibilmente complessi, come quelli che guidano le auto autonome.

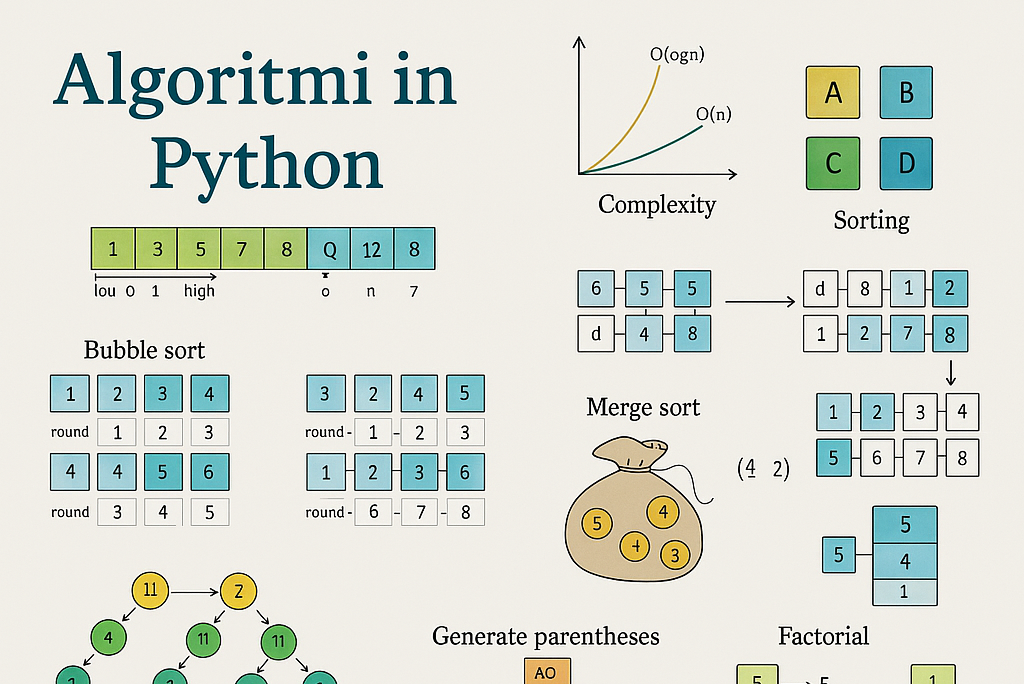
Nell’immagine che hai condiviso, vediamo un assaggio di questo mondo affascinante. Partiamo da lì per esplorare alcuni tipi di algoritmi, vedere come si scrivono in Python e scoprire dove li incontriamo ogni giorno (spesso senza nemmeno accorgercene!).

La Ricerca Veloce: Binary Search (Ricerca Binaria)

Hai una lista ordinata di numeri (proprio come quella nell’immagine: 1, 3, 4, 7, 10, 11, 13) e devi trovare un numero specifico, diciamo il 4. Potresti controllarli uno per uno (ricerca lineare), ma se la lista fosse lunghissima? Che noia!

Qui entra in gioco la Binary Search. L’idea è geniale nella sua semplicità:

1. Guarda il numero al centro della lista (nell’esempio, è il 7).
2. Il numero che cerchi (4) è più piccolo o più grande? Più piccolo.
3. Allora ignora tutta la metà destra della lista! Non ci serve più.
4. Ripeti il processo sulla metà sinistra rimasta (1, 3, 4). Il centro è 3.
5. Il 4 è più grande. Ignora la metà sinistra (solo l’1).
6. Rimane solo il 4. Trovato!

Vedi come abbiamo dimezzato il campo di ricerca a ogni passo? Questo rende la Binary Search incredibilmente veloce, specialmente su grandi quantità di dati. Nell’immagine, vedi quel grafico della “Complexity”? La Binary Search ha una complessità O(log n), che significa che anche se la lista diventa enooorme, il tempo per trovare l’elemento cresce molto lentamente. Figo, vero?

Applicazioni nel mondo reale:

• Ricerca di un contatto nella rubrica del telefono (che di solito è ordinata alfabeticamente).
• Suggerimenti di completamento automatico durante la digitazione.
• Verifica se un nome utente è già stato preso durante la registrazione a un sito.

Python in azione (semplificato):

def binary_search(lista_ordinata, elemento_da_trovare): basso = 0 alto = len(lista_ordinata) - 1 while basso <= alto: meta = (basso + alto) valore_centrale = lista_ordinata[meta] if valore_centrale == elemento_da_trovare: return meta # Trovato! Restituisce l'indice elif valore_centrale < elemento_da_trovare: basso = meta + 1 # Cerca nella metà destra else: alto = meta - 1 # Cerca nella metà sinistra return None # Elemento non trovato # Esempio d'uso: numeri = [1, 3, 4, 7, 10, 11, 13] indice = binary_search(numeri, 4) if indice is not None: print(f"Elemento trovato all'indice: {indice}") else: print("Elemento non trovato.") 

Mettere Ordine: Algoritmi di Ordinamento (Sorting)

L’immagine ci mostra due modi per mettere in ordine una lista: Bubble Sort e Merge Sort.

• Bubble Sort: È il classico esempio che si insegna per primo. Immagina le bollicine (bubbles) che salgono: l’algoritmo confronta coppie di elementi adiacenti e li scambia se sono nell’ordine sbagliato. Ripete questo processo finché tutta la lista è ordinata. È semplice da capire (vedi i passaggi “round 1, round 2…” nell’immagine), ma non molto efficiente per liste grandi (O(n²) nel grafico della complessità, la curva che sale più rapidamente).
• Merge Sort: Questo è più furbo. Usa una strategia “Divide et Impera”:
  1. Divide: Spezza la lista a metà, poi ancora a metà, finché non hai tante piccole liste con un solo elemento (che sono, ovviamente, già ordinate).
  2. Impera (Conquer/Merge): Ricombina queste piccole liste in liste ordinate più grandi, confrontando gli elementi tra loro. Alla fine, otterrai l’intera lista perfettamente ordinata. L’immagine lo illustra bene con le fasi “divide” e “merge”. È molto più efficiente del Bubble Sort (O(n log n)).

Applicazioni nel mondo reale:

• Ordinare i prodotti su un sito e-commerce per prezzo, popolarità, ecc.
• Ordinare le email per data o mittente.
• Classifiche di punteggi nei videogiochi.

Python in azione (Bubble Sort per semplicità):

def bubble_sort(lista): n = len(lista) scambiato = True while scambiato: scambiato = False for i in range(n - 1): if lista[i] > lista[i+1]: # Scambia gli elementi lista[i], lista[i+1] = lista[i+1], lista[i] scambiato = True # Ottimizzazione: riduce il range ad ogni passaggio # perché l'elemento più grande è già "galleggiato" alla fine n -= 1 return lista # Esempio d'uso: disordinata = [2, 8, 1, 5, 3] ordinata = bubble_sort(disordinata.copy()) # Lavora su una copia per non modificare l'originale print(f"Lista disordinata: {disordinata}") print(f"Lista ordinata: {ordinata}") 

(Nota: Python ha una funzione sort() e sorted() super ottimizzata integrata, che probabilmente usa un algoritmo chiamato Timsort, un ibrido efficiente!)

L’Arte di Chiamare Sé Stessi: Ricorsione

La ricorsione è un concetto affascinante: una funzione che, per risolvere un problema, chiama sé stessa con una versione leggermente più piccola dello stesso problema. Pensa a delle matrioske! L’immagine mostra alcuni esempi classici:

• Fattoriale (Factorial): Per calcolare il fattoriale di 5 (5! = 5 * 4 * 3 * 2 * 1), la funzione fattoriale(5) chiama fattoriale(4), che chiama fattoriale(3), e così via, fino a fattoriale(1) (il caso base). L’immagine mostra proprio lo “stack di chiamate” (call stack) che tiene traccia di queste chiamate.
• Generare Parentesi (Generate Parentheses): Trovare tutte le combinazioni valide di parentesi (es. per n=3, ((())), (()()), (())(), ()(()), ()()()). Anche qui, la ricorsione esplora le varie possibilità aggiungendo ‘(‘ o ‘)’.
• Distanza di Edit (Edit Distance): Calcolare il numero minimo di modifiche (inserisci, cancella, sostituisci carattere) per trasformare una parola in un’altra (es. da “BALL” a “SAW”). La ricorsione esplora le diverse sequenze di modifiche.

Applicazioni nel mondo reale:

• Navigazione in strutture ad albero, come le cartelle del tuo computer.
• Algoritmi di “backtracking”, usati per risolvere puzzle come il Sudoku.
• Alcuni algoritmi grafici, come la generazione di frattali.

Python in azione (Fattoriale):

def fattoriale_ricorsivo(n): # Caso base: il fattoriale di 0 o 1 è 1 if n == 0 or n == 1: return 1 # Passo ricorsivo: n * fattoriale(n-1) else: return n * fattoriale_ricorsivo(n - 1) # Esempio d'uso: num = 5 risultato = fattoriale_ricorsivo(num) print(f"Il fattoriale di {num} è: {risultato}") 

Curiosità: La ricorsione può essere elegante, ma attenzione! Se non definisci bene il “caso base” (la condizione per fermarsi), la funzione continuerà a chiamare sé stessa all’infinito, portando a un errore chiamato “stack overflow”. È come una matrioska senza l’ultima bambolina!

Ricordare per Risolvere: Programmazione Dinamica (Dynamic Programming)

A volte, un problema complesso può essere scomposto in tanti sotto-problemi più piccoli che si ripetono. La ricorsione “pura” potrebbe finire per ricalcolare la stessa cosa più e più volte, sprecando tempo.

La Programmazione Dinamica (DP) è una tecnica potentissima per ottimizzare questi scenari. L’idea chiave è: risolvi ogni sotto-problema una sola volta e memorizza il risultato. Se ti serve di nuovo, vai a ripescare il risultato salvato invece di ricalcolarlo. È come prendere appunti mentre risolvi un grosso puzzle!

L’immagine mostra:

• Problema dello Zaino (Knapsack): Hai uno zaino con una capacità limitata e una serie di oggetti, ognuno con un peso e un valore. Quali oggetti scegliere per massimizzare il valore totale senza superare la capacità? La DP aiuta a esplorare le combinazioni in modo efficiente.
• Distanza di Edit (Edit Distance): Sì, di nuovo lei! La DP è un modo molto comune ed efficiente per risolvere questo problema, spesso usando una tabella (proprio come quella griglia nell’immagine) per memorizzare le distanze tra sotto-stringhe.

Applicazioni nel mondo reale:

• Bioinformatica: Allineamento di sequenze di DNA o proteine (trovare somiglianze).
• Routing: Trovare il percorso più breve in una rete (alla base di app come Google Maps).
• Finanza: Modelli di pricing per opzioni finanziarie.
• Correttori ortografici: Suggerire la parola corretta più “vicina” (minor distanza di edit).

Python in azione (Fibonacci con memoization – un tipo di DP): La sequenza di Fibonacci (0, 1, 1, 2, 3, 5, 8…) è un classico esempio. fib(n) = fib(n-1) + fib(n-2). Una versione ricorsiva semplice ricalcola fib(2), fib(3) ecc. un sacco di volte. Con la DP (memoization):

# Dizionario per memorizzare i risultati già calcolati memo = {} def fibonacci_dp(n): # Se il risultato è già in memoria, restituiscilo if n in memo: return memo[n] # Caso base if n <= 1: return n # Calcola, memorizza e restituisci risultato = fibonacci_dp(n - 1) + fibonacci_dp(n - 2) memo[n] = risultato return risultato # Esempio d'uso: num = 10 print(f"Il {num}-esimo numero di Fibonacci è: {fibonacci_dp(num)}") print(f"Risultati memorizzati: {memo}") 

Vedrai che fibonacci_dp(10) è molto più veloce di una versione puramente ricorsiva per numeri grandi, perché riutilizza i valori già calcolati!

Un Mondo da Esplorare

Come vedi, gli algoritmi sono molto più di semplici istruzioni per computer. Sono strategie intelligenti per risolvere problemi, ottimizzare processi e, in definitiva, rendere la nostra vita digitale (e non solo) più efficiente e interessante. Dall’ordinare una semplice lista alla complessità della programmazione dinamica, Python ci offre gli strumenti per sperimentare e costruire.

L’immagine che hai fornito è solo la punta dell’iceberg. Ci sono tantissimi altri algoritmi affascinanti là fuori: algoritmi per grafi (come quelli usati dai social network per suggerire amici), algoritmi di machine learning (il cuore dell’intelligenza artificiale), algoritmi crittografici (che proteggono i nostri dati)…

Il bello è che non devi essere un mago dell’informatica per iniziare a giocare con gli algoritmi in Python. Ci sono risorse infinite online, tutorial e librerie che possono aiutarti.

Quindi, la prossima volta che usi un’app o un sito web, prova a immaginare quali algoritmi potrebbero essere al lavoro dietro le quinte. E perché no? Magari prova a implementarne qualcuno tu stesso in Python. Potresti scoprire una nuova passione!

E tu, quale di questi concetti ti ha incuriosito di più? C’è qualche applicazione particolare degli algoritmi che ti affascina? Il viaggio nel mondo degli algoritmi è appena iniziato!